On Compound Interest

Observations on exponential growth and its affects on investment returns.

Published: Sep 2017|Revised: May 2021

This article has charts and some interactive elements. Reading on a bigger screen might get you more out of the article.

Exponential growth is unintuitive See: Exponential Growth Arithmetic, Population and Energy (video) talk by Al Bartlett. But thankfully, there are tricks which help in understanding implications of different rates of growth. The trick is finding doubling period, and number of doublings. If you are only interested in the trick, jump to Mental math. Rest of the article goes through various properties of compounding curve by looking at the equation (and charts) behind itArticle is not a financial advice. Doesn't cover risk, real Interest rate, taxes, or other factors that affect investments. Rather, we will go through rough calculations with intent is to understand broad behavior, and not details.. It's simple observations, but I haven't found a similar coverage elsewhere. Article does assume familiarity with basic maths. Multiplication and equational reasoning should be enough to understand most of it.

Motivation

To motivate why you should care, here is a made up scenario. You want to invest $1,000 today and found two options both offering annual interest rate of 10% for 30 years. Your two options are, investment with annual interest paid back to you (I will call this dividend based investment in rest of the article), or compounding interest. Which one would you opt for? Here are the approximate returns to help you decide.

Dividend: $1000 + (100 * 30)$ $4,000
Compounding: $1000 * (1 + 0.1)^{30}$ $17,000

Here is another hypothetical scenario. You have a friend same age as you. Your friend invested $1,000 at the age of 20. You being lazy, invested your first $1,000 at the age of 30 (10 years after your friend). Both investments compound at 10% annual interest rate. How much would your respective investments grow to, when you both are 60 years old?

your friend: $1000 * (1 + 0.1)^{40}$ $45,000
you: $1000 * (1 + 0.1)^{30}$ $17,000

If you delayed your investment by another 5 years (invested at age 35), the return would have been even lower: $1000 * (1 + 0.1)^{25}$ $11,000 .

Compounding is unintuitive but has real and significant implications. We will explore some of it's characteristics in this article.

There are some interactive parts in the article.

Numbers which show up like
can be clicked. It opens up a slider to change the number.
Hovering over charts shows some details.
Text styled like over note showing some detailsthis would show some details on hover (click on mobile/tablet).

Summary

Some financial wisdom, which are based on the compound interest equation:

Compounding is exponential process.
- Time matters. Invest earlyIf you start investing at the age of 20, and don't touch the money till 60, you can utilize 40 years of compounding. Later you start, less years for compounding..
- Every percent in interest rate matters.
Splitting investment, other things being same, doesn't affect return. A good way to manage risk.

Mental math

If you like doing back-of-the-envelope calculations, you might find these tricks useful.

Rule of 72: $72/r$ is an approximation on the doubling period of an investment. But this doesn't give you an idea of time value of the investment.
Doublings: Each doubling period, money doubles. $\frac{investment\ period}{doubling\ period}$ $\frac{in v es t m e n t p er i o d}{d o u b l in g p er i o d}$ would give you doublings. And $2^{doublings}$ $2^{d o u b l in g s}$ would roughly give the multiple by which the investment would grow. This is simpler to calculate if $investment\ period$ $in v es t m e n t p er i o d$ is a multiple of $doubling\ period$ $d o u b l in g p er i o d$ . Few examples of back-of-envelope approximations:
- 10% investment over 35 years. Doubling period is $\frac{72}{10}$ 7 years. Number of doublings, $\frac{35}{7}$ 5. Investment grows by $2^5$ 32.
- 7% has doubling period of 10 years. In 30 years, the investment should grow
  $2^\frac{investment\ period}{doubling\ period}$
  $\rightarrow 2^\frac{30}{10}\\\rightarrow 2^3$
  8 times. In 40 years, investment should grow
  $2^\frac{investment\ period}{doubling\ period}$
  $\rightarrow 2^\frac{40}{10}\\\rightarrow 2^4$
  16 times.

Characteristics of compounding investments

Now to the main content. We will start with what compounding and dividend based investment mean in this article. Then look at the equation and curves etc.

Compounding and dividend

Dividend based investment, in this article, is used for investments where the interest doesn't get reinvested. You invest $1,000, but each year, take out the interest.

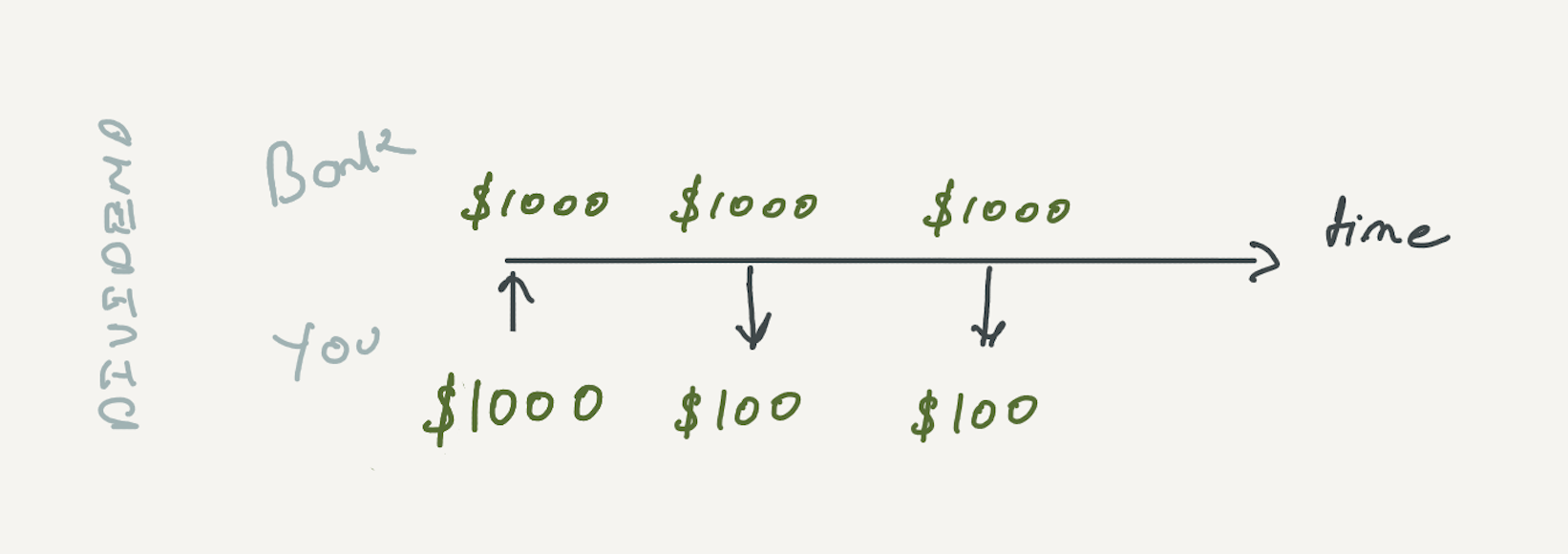
By the end of two years, you would have $1,000 + $100 + $100, or $1,200

In case of compound interest approach, interest made is put back into investment (or is not taken out of the investment).

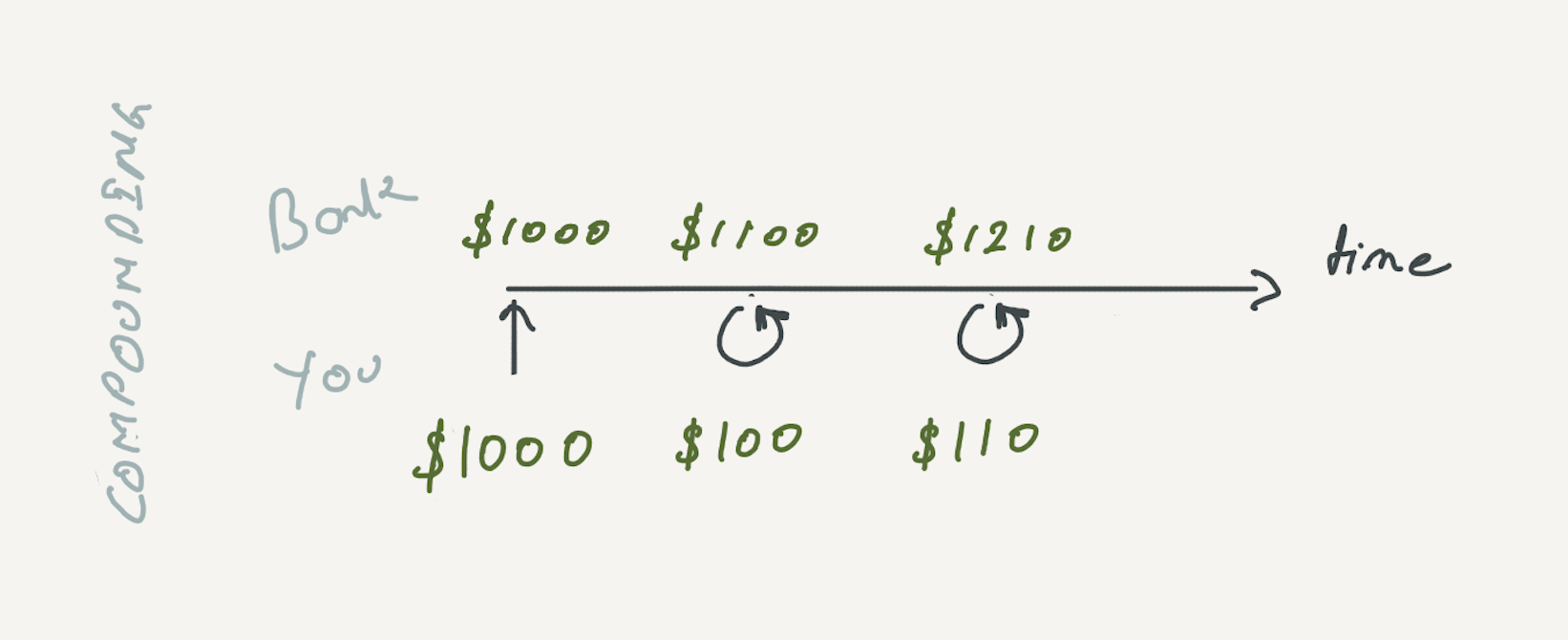
In this case, by end of 2nd year, you would have $1,000 + $100 + $110, or $1,210. The difference at 2 years is small. But with time, compounding would return significantly more.

You can learn more about compound interest at Khan Academy.

Equation

Let's first understand the equation for compounding. To understand the equation, let's say you invest $100, with an interest rate of 10%. We will use 10% interest would mean $r$ is 0.10 $r$ for rate of interest, $n$ for the number of years, $P$ for the initial amount and $P'$ for amount at the end of year $n$ . Every year, you get interest on money that was there at the starting of the year. E.g.

\begin{align} &money\ at\ year\ end\ \\& =\ money\ at\ year\ start\ + \\&\ \ ( money\ at\ year\ start\ *\ rate\ of\ interest )\\ \end{align}

For the first year:

\begin{align} {1^{st}\ year} &= 100 + 100*0.10 \\ &= 100 * (1 + 0.10) \\ &= P * (1 + r) \\ \end{align}

For the second year:

\begin{align} {2^{nd}\ year} &= {1^{st}\ year} + {1^{st}\ year}*0.10 \\ &= {1^{st}\ year} * (1 + 0.10) \\ &= 100 * (1 + 0.10) * (1 + 0.10) \\ &= 100 * (1 + 0.10)^2 \\ &= P * (1 + r)^2 \\ \end{align}

And so on. If you invest amount $P$ with an annually compounded interest $r$ , in $n$ years the total amount $P'$ would be:

P' = { P(1 + r)^n }

For dividend based investments, the equation would be:

D' = D(1 + r*n)

Multiple

First thing to note is that the return $P'$ is a multiple of initial investment $P$ . All the observations in the article depend on this property. In other words, we can write the equation as:

\frac{P'}{P} = { (1 + r)^n }

This means, In terms of growth rate, it doesn't matter whether you invest $100 or $100,000. They both grow in the same way. What matters is the interest rate. E.g. if the interest rate is 7%, in the first year both of them would grow to 1.07 times the initial value. In the second year, both of them would be approximate $(1 + 0.07)^{2}$ 1.14 . In the third year, both of them would be approximate $(1 + 0.07)^3$ 1.23 times the initial value. So, for the same interest rate, the more money you put in, the more returns you get.

With interest rate, in years your initial investment would grow approximately times. In other words:

$1,000 would grow to $0.
$1,000,000 would grow to $0.

Another nice property is thatGiven interest rate and duration is same. you can split the money into multiple investments and get the same returns . Ex, you could replace $P$ with $P_1 + P_2 + ... + P_n$

P' = (P_1 + P_2 + ... + P_n){ (1 + r)^n }

This is a good way to manage risk. High interest usually comes with high risk. Putting all the money in a single investment would mean loosing all the money if the fund goes down. Instead, the money could be invested in multiple funds.

The multiple property is applicable for dividend based investments also. E.g.

\frac{D'}{D} = (1 + r*n)

Rule of 72

doubling\ period = { 72 \over interest\ rate }

This is a way to approximate the doubling time of investment.

With an interest rate of , in years (which is approximately 72/) your initial investment will double.

Again (I find it interesting and worth repeating): doubling period doesn't depend on how much money you put in. Put as much as you can, you will get double of it, after a doubling period.

Doubling continues

The Rule of 72 gives us a number to compare. It's one doubling time. An important but unintuitive number. With every doubling time, your investment doubles. After $x$ doubling periods the investment would be $2^{doubling\ period}$ times it's original amount. E.g. doubling time of interest rate of 100%1 year and interest rate 18%4 years don't seem too far apart. But in 12 years, doubling time of 1 year would return $2^\frac{12\ years}{1\ year}$ 4096 times the original amount. While doubling time of 4 years would return $2^\frac{12\ years}{4\ years}$ 8 times the original amount.

interest rate has doubling period of approx years. By year (3 doubling years), your investment would grow to 8 times the initial investment. And if you wait another years, it will grow to 16 times.

Dividend based investment doubles in $\frac{100}{r}$ yearsPlay with $D' = D( 1 + r * n)$ to reason why.. Although it is larger than in case of compounding based investment, but the real difference comes because of continued doubling. Next doubling in dividend happens in $\frac{300}{r}$ . And this keeps increasing for future doublings. For compounding, doubling period remains same. And after $x$ doubling periods, investment would return $2^{x}$ times initial investment. That is the significant difference.

Value of 1%

What difference does a 1% change in interest rate make? Hover over the plot below to see the doubling time for the interest rate.

Notice how when interest rates are low, 1% makes a big difference in doubling period. This was a surprise to me. Although this does mean that 1% matters more for returns, when interest rate is low. Every 1% matters, no matter what interest rate you are getting :)

Lets say your investment is giving you interest rate and the management fees is . That 0% is increasing your investments doubling period by approximately 0 years.

Value of interest rate

The chart below shows return curves for different interest rates. The higher the interest rate, the steeper the curve.

Here is a way to think about it, in terms of doubling period. Lets compare interest rates of (which has doubling period of years) and (which has doubling period ). Difference between their doubling period is NaN. For your money to grow 8 times, requires 3 doubling periods. In other words, % investment would take NaN (3 × NaN) years more than investment with % interest rate , to grow your money by 8 times.

Value of time

Each of the curves below represents a time period (ex: 40, 30, 20 years). The x-axis is the interest rate, and y is the multiple of the investment. Again, the longer you let your investment grow, the bigger the returns. Note how fast the curve grows for high-interest rates and long periods.

With an interest rate of 12%, after 40 years, your investment would have grown 100 times!

In one table

Here is a table of interest rates, years and returns (as multiple of initial amount) associated with that. The top right cell represents 25% annual interest compounded for 35 years. Initial amount would grow 2500 times. Let's say you invested $1,000. That would become $2,500,000.

Value of maths?

Much of what we figured out, is just maths and looking at curves. Let's play around with it a little more.

Where does 72 come from?

We will attempt a close enough answer. Let's look at our equation again.

\frac{P'}{P} = { (1 + r)^n }

Doubling means $P' = 2*P$ , or $\frac{P'}{P} = 2$ . In other we need to solve for:

2 = { (1 + r)^n }

Taking natural log on both sides.

ln(2) = { n * ln(1 + r) }

n = { ln(2) \over ln(1 + r) }

Now here is a nice trick. Turns out, for small values of $r$ , $ln(1 + r)$ is approximately $r$ . Ex, $ln(1.01)$ it's 0.01, for $ln(1.2)$ it's 0.18, approximately. So, for most practical interest rates, we could just use:

n = { ln(2) \over r }

$ln(2)$ turns out to be 69, so doubling time could be equated to (approximately)

n = { 69 \over r }

But we have been using 72! Wiki explains the reasons behind choosing 72 (or 70 or 69).

Slopes

Let's again start with the compound interest equation $(1 + r)^n$ . For a curve, the slope at a point is one way of figuring out how fast change is happening at that certain point. A point in the curve represents some point in time and the change in return at that time. With the slope of the curve, if we assume it to be the same for a year around the point, we can approximate the rate of return in that year, by calculating the change in return.

Derivative gives us the slope curve. Derivative of the compound interest equation:

{ \frac{d(1 + r)^n}{dn} } = { ln(1 + r)(1 + r)^n }

We learned earlier that for small values of r, $ln(1+r)$ could be replaced with $r$ . So, we could write the above equations as:

{ r(1 + r)^n }

Now, let's consider what this means.

Lets take an investment with interest rate . What would be the growth of the investment in year ? The investment would have grown to 1.00 the initial amount, at the starting of . The slope of the line at the middle of the year, ex 0.5, is

r(1+r)^{0.5}

, which is (as percentage) 0.00%. The actual change between year and 1 is 0.00%.

Play around with different interest rates and year values. The approximation is mostly within 1% of the values in real life.

This also gives us a quick way to approximate the percentange change in the year when the amount doubles (or quadruples, or other powers of 2). At the year of the doubling,

(1+r)^n

is 2. So the rate change that year comes out to be

r\times2

. Ex, for interest rate , it would be 0.00 × 2 or 0%. On the year of the second doubling it would be 0.00 × 4 or 0%.

Some thoughts around exponentials

It's relatively easy for our brains to think of linear processes. E.g. what would be your age in 10 years?current_age + 10 Or you get $100 every year as dividend on your investment, how much dividend would you get in total, after 10 years?$1,000 Exponential processes (like compounding) on the other hand, are not as intuitive, but could have a much bigger impact on our life.

Exponential growth is a process where the growth in quantity is proportional to its current value. E.g. when we say the population is growing 2% every year, we mean the population grows by 2% of what it was, at the starting of that year. Covid-19 growth is proportional to the affected people, given enough population and no preventive measures. Knowledge grows exponentially. If you improve on something by 1% every day, by end of the year, you would be about 36Try doing back-of-the-envelope to arrive at greater than 32 times? Close enough to prove the point. times better than when you started.

What now?

There are many factors to consider for personal finance and investment. Mostly they come down to risk and return (which includes the interest rate, taxes, management fees, entry and exit fees, etc). Personal finance is a big topic. You could probably start by reading discussions at Personalfinance subreddit. But remember, to get the most out of compounding, invest early.

Also, it's interesting to note that throughout the article, all we did was look at the implications of the equation $P' = P(1 + r)^n$ .

Pointers to explore more

Time value of money
Rule of 72
Exponential Growth Arithmetic, Population and Energy (video) talk by Al Bartlett
Functions and Graphs by I. M. Gelfand, E. G. Glagoleva, E. E. Shnol. A nice book on properties of functions and graphing them.
Tools
- Desmos - A tool to chart equations.
- GeoGebra
- If you are on macOS, Grapher.app is also good.

Acknowledgment

Thanks to Saneef, Rahul, Anantha Kumaran, Rohit Shinde and many others for their feedback.

...