On Time, clock and ordering paper

Time, Clocks and Ordering (TCO) paper is among the most referred paper in distributed systems. Often, summaries/discussions about the paper concentrate on the logical clock. Logical clock is an important contribution of the paper. But more interesting part is being able to implement arbitrary distributed state machines, given the no-failure assumption. Moreover, personally I find the paper to be a gateway drug to distributed systems. A way to give structure to some topics in distributed systems.

The paper shows how to implement an arbitrary state machine with distributed process, assuming there are no failuresHow does failure affect distributed systems. We will look at it briefly in the observations section.. Failures are unavoidable in real systems. Which makes this approach of deterministic distribute state machine impractical. Nevertheless the model used to prove the result is still quite useful.

It didn't take me long to realize that an algorithm for totally ordering events could be used to implement any distributed system. A distributed system can be described as a particular sequential state machine that is implemented with a network of processors. The ability to totally order the input requests leads immediately to an algorithm to implement an arbitrary state machine by a network of processors, and hence to implement any distributed system. So, I wrote this paper, which is about how to implement an arbitrary distributed state machine. As an illustration, I used the simplest example of a distributed system I could think of a distributed mutual exclusion algorithm.

-- 27. Time, Clocks and the Ordering of Events in a Distributed System (Emphasis mine)

If you understand that statement, please feel free to jump to the observations sections, and ignore rest of the article.

The Model

In the paper distributed system is modeled as a set of processes communicating with (passing messages to) each other. One way to make such a system deterministic, is to make parts of the systemin this case processes and communication deterministic and combine them in deterministic way.Are there other ways to make system deterministic? See observations for some discussion. This statement might become clear as we go through the article.

Let’s consider processes first. How do we make processes deterministic? A common approach is to model processes as state machinesDeterminism implies that the process can't read clocks or random numbers or cursor position etc. Or at least, they are modeled as input to the system. with messages as being the commands to the state machines. If you haven’t come across state machines, please do read the wiki on it. The intuition is, given initial state, and same sequence of commands, state machine will reach the same state every time you execute it (it’s like a pure function over initial state and sequence of commands).

With processes being deterministic, the only non-determinism that remains in the system, is the order of messages. With network delays, when a message arrives is not deterministic. But, if we can make sure that all processes (which are state machines) execute messages (commands) according to a global order, then we would have a deterministic system. The algorithm is slightly more involved, and covered later in the article.

Before that, how do we get total order for messages. One way is to have a central server to sequence eventsThis is not a distributed algorithm, although, don't rule this out. Many practical distributed systems use some version of this.. Instead, and this is the most interesting part of the paper, the paper describes how we can have globally ordered events, with only local decisions. Thats the purpose of logical clocksCould we use real clocks (all computers have clocks) for ordering events? Well, yes and no. See Real world needs clocks and observations sections for more. . First few sections of the paper are about deriving logical clocks, to get global order for events. Which is then used to build a deterministic distributed mutual exclusion algorithm.

With the context in mind, here is roughly the structure of rest of the post (which mimics the paper).

1. Events
   1. Partial Ordering Define which orders need to be preserved. Paper calls these happened-before relations (e.g. all events in a process are ordered, and messages define ordering between processes).
   2. Logical Clocks Define properties that a logical clock would have to satisfy, to capture causality (the happened-before relations).
   3. Total Ordering Use logical clock and process ordering to get total order.
2. Deterministic Distributed System Use state machine processes and total ordering to define an algorithm for mutual exclusion without any central server or storage.

I will conclude with some Observations around how it connects with other topics in Distributed systems.

1. Events

Events relevant for the paper, are the events around sending and receiving messages. For more details, please read the paper. You could also refer to a more formal coverage at Lamport's Logical Clocks. In all the pictures below, time flows to the right and the horizontal lines represent the different processes (or humans).

1.1 Partial Ordering

First we need to understand which orders are important to preserve. There are primarily two cases. First, events happening in a single process, are ordered. E.g a user request message was received before the database query message being sent to another process. Second, if process $p_1$ sends a message to process $p_2$, intuitively, events that happened before $p_1$ sends the message, should happen before, events in $p_2$ after it has received the message. These causal relations are formalized in the paper, as below:

1. 
   If $a$ and $b$ are events in the same process, and $a$ comes before $b$ , then $a \rightarrow b$ .
2. 
   If $a$ is the sending of a message by one process and $b$ is the receipt of the same message by another process, then $a \rightarrow b$.
3. If $a \rightarrow b$ and $b \rightarrow c$ then $a \rightarrow c$. Two distinct events $a$ and $b$ are said to be concurrent if $a \nrightarrow b$ and $b \nrightarrow a$.

Here is an example with two process communicating. $a$ sends a message $m_1$ to $b$, which after some processing, sends back message $m_2$ to $a$. An event happened before another, is there is a sequence of happened before relations connecting them. Few relations: $c \nrightarrow b$ (there is no happened-before relation between $c$ and $b$), $c \nrightarrow d$, $a \rightarrow d$ ($a$ happened-before $b$).

1.2 Logical Clocks

The happened-before relations can be mapped to numbers (which are comparable). This would help with implementing them in real systems. The two conditions in the Logical Clocks section define the constraints that such representation should adhere to.

• C1 If $a$ and $b$ are events in process $P_i$, and $a$ comes before $b$, then $C_i \langle a \rangle < C_i \langle b \rangle$
• C2 If $a$ is the sending of a message by process $P_i$ and $b$ is the receipt of that message by process $P_j$, then $C_i \langle a \rangle < C_j \langle b\rangle$.

Now, what kind of mapping could work for this? Essentially, increment for any event within a process. and if a message is sent, increment before sending. The message itself carries the logical clock timestamp of the sending process. And the receiving process picks a time stamp greater than both the message and its current time stamp max(clock_in_msg, local_clock) + 1. This gives an ordering of the all the messages for which the order needs to be preserved.

Here is a mapping for the happened-before relation we saw earlier. Note that the timestamp for both $c$ and $b$ is same, 2. This can happen for some of the events across processes, which are not related by happened-before. Which means, we still don't have total order.

1.3 Total order

The few cases where timestamp might be same for events across processes (similar to last section), we need a deterministic way to order them. The approach paper uses is to have a pre-determined order for processes. So the total order is given by the pair (time-stamp, process_id). If the logical timestamp clashes, we break the tie with process_id. For the events below, if $p < q$, where $p$ and $q$ are process_id for the respective processes, then the global order of events is $(1,p) \rightarrow (2, p) \rightarrow (2,q) \rightarrow (3,q) \rightarrow (4,p)$

To summarize, we have total order for all the messages and given two events, any process can derive their global order only based on their timestamps and the predefined order of processes.

2. Deterministic Distributed System

We are ready to combine this total order and state machines, to create an arbitrary state machine on a distributed system (set of processes). The paper shows this by implementing a distributed mutual exclusion algorithm.

You should read the paper for the algorithm, but here is my intuition. First the assumptionsAlthough, they might not be necessary. E.g. One can build a reliable messaging service (like tcp) over reliable processes.:

1. Messages between two processes are received in order.
2. Messages are eventually delivered

Moving on to the algorithm, the intuition that helps, is to look at the process locally. Consider a process $P_i$ which has its request as the lowest timestamp on the request queue. Let's say the request has timestamp $ts_i$. Let's also consider another process $P_j$. If $P_i$ has received a message from $P_j$ with timestamp greater than $ts_i$, then $P_i$ can be sure that no other message with lower timestamp can come from $P_j$. Similar logic applies to all the other processes. So, $P_i$ executes its request, when its command has the lowest timestamp in the request queue and it has received messages with timestamp greater than $ts_i$ from all the processes.

Here is an example. The green events are the message send events for mutual exclusion request. The brown events are message send events after the mutually exclusive block. The green segment of process timeline signifies the time range where the command would be executed. For this example, let's assume $p < q < r$, with $p$, $q$, $r$ being the process_id for processes $P$, $Q$, $R$ respectively. Note that the first event for both process $P$ and $Q$ have first request event with timestamp 1. Since $p < q$, $(1,p) \rightarrow (1,q)$.

The same execution is show below with only a subset of events and messages highlighted, which are related to $(1,p)$ request.

Now, the same execution with subset of events and messages relevant for $(1,q)$ highlighted.

Notice how even though the requests are happening concurrently and process $R$ received request from $Q$, before request from $P$, $P$ completes it's mutually exclusive execution $Q$.

Implementing an arbitrary state machine should also be straight forward. E.g. mutual exclusion could be used to decide on which command is executed next, across the state machines. Hence implementing replicated state machine. Although, it could be made slightly faster by send acknowledgement to all process. See Concurrency: The Works of Leslie Lamport

Real world needs clocks

Note also that the algorithm is distributed in the sense that state machine is only cares about sequence of events, not when it happens. But some events might have a happened-before relation in the physical world. E.g you transferring money to a friend and calling them to check it on their end.

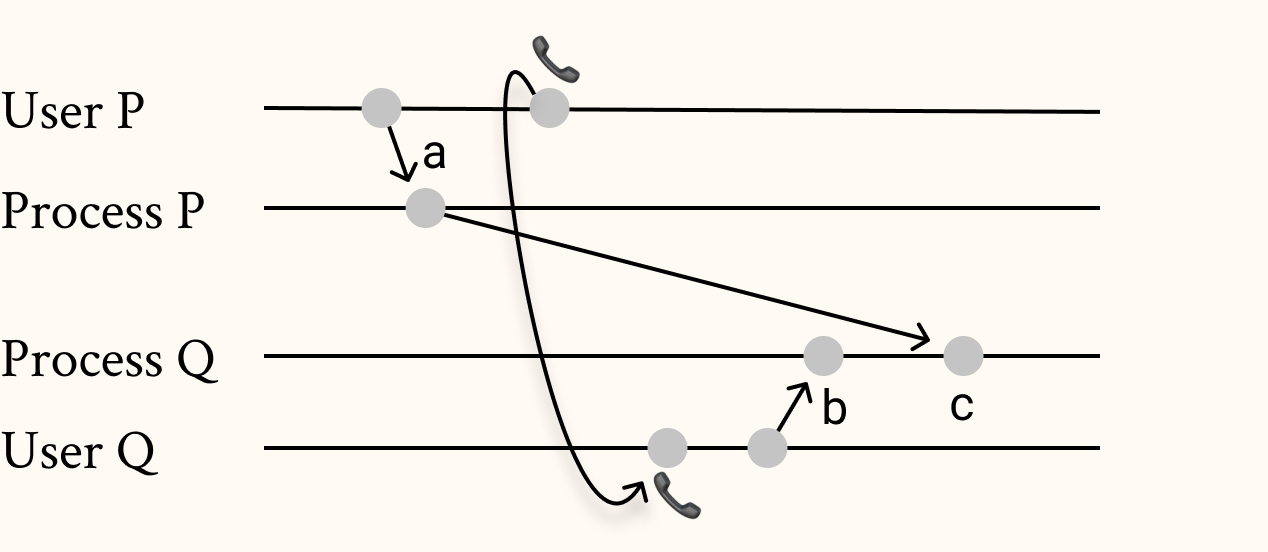
Lamport points out that synched clocks could be used to preserve happened-before relations outside of the system. As an example, with the mutual exclusion algorithm above, the user commands could be run based on the total order (which uses synched clock for timestamps). This would mean, event $b$ would be run by the state machine after event $c$ since $c$'s timestamp would be smaller than $b$.

Observations

I like to think of TCO paper as a gateway drug to distributed systems. This section might feel a little contrived. But the associations help me think, so why not. I am just starting to explore these topics myself, slowly. So, read it with more skepticism. I will link a few resources which might help with exploring the topics.

• Models of Distributed system: For thinking about distribute systems, it helps to understand the model on which the theory builds. E.g in this paper, the models used is asynchronous communication and no-failure. Asynchronous communication is realistic, but no-failure is not. Communication could be asynchronous, synchronous or semi-asynchronous. Failures can be fail-stop, crash, crash-recovery, Byzantine etc. Understanding the assumptions, helps create a mental model of what is applicable where. In particular, pay close attention to models used in impossibility (see FLP Impossibility below), or in proofs on consensus algorithms. See these lecture notes for some coverage on different models. Realistic model might be semi-asynchronous with crash-recovery.

• Logical clock: the clock described in the paper is usually known as Lamport timestamps. More logical clocks have been formulated. E.g. vector clock, which helps detecting causal relations (Lamport clock only keeps the relation). Check out the wiki on logical clocks.
• FLP Impossibility: The model used in TCO paper assumes no-failure. What happens if failure is part of the model (e.g. more realistic systems)? Turns out, with asynchronous networks and crash fail, consensus can't be guaranteed. But this doesn't mean consensus can't be achieved. The proof for this seems interesting.
• Consensus: Consensus is an important part of distributed system. Although FLP impossibility means consensus can't be guaranteed, but I think the worst case happens only if there is an oracle which knows exactly when to slow down a process. Practically, consensus is used a lot, in fact in almost all distributed systems, consensus algorithms might be involved in one way or the other. In the original paxos paper, this is the synod algorithm.
• Replicated state machine: If you read papers on consensus, you will come across replicated state machines a lot. One could implement a deterministic state machine on a single machine. But to be reliable (in case of failure), data needs to be replicated to more than one machine. Naive implementation of this might lead to inconsistent data on different machines. To have consistent data with replication, consensus is needed (where a set of machines agree on what the current state of the system is). Most protocols like Paxos, Raft maintain a log and use consensus to append to it across the state machines. You could read A Generalized Multi-Leader State Machine Replication Tutorial, which refers more papers on the topic.
• CRDT: Replicated state machines allow for generic fault tolerant systems. It does this by having consensus on append to a command log. But if the commands are commutative, those could be applied in any order. There is subset on optimizations on paxos for concurrent commutative commands, called Generalized Paxos. In the extreme case, if all operations are commutative, then you have this nice situation where you don't need consensus. And replicas can converge on the same state, eventually. These data structures with commutative operations are called CRDT. [video] Strong Eventual Consistency and Conflict-free Replicated Data Types -- Marc Shapiro
• Clocks: Even with no-fault assumption, TCO paper still points out that clocks are important, to capture the causal relations that are not part of the system. This is an important part of distributed system. Example, Spanner uses synchronized clocks to guarantee that even external causal relations are maintained.

More references

• Oral History of Leslie Lamport - Part 1
• Keeping Time in Real Systems by Kavya Joshi
• Distributed Systems lecture series by Martin Kleppmann

Acknowledgement

Thanks to Akash, Rahul, Rohit Shinde and others for their feedback.